Suppose we have a pair of stars orbiting each other in a binary system. Each star has a Roche lobe, beyond which matter is not gravitationally bound to the star. What happens if one of the stars grows larger than its Roche lobe? Since this material is no longer bound to the original star it is clear that mass will be lost from the original star and it is likely that the secondary will accrete some or all of the matter. But over what timescale will this mass transfer take place? This is the question addressed in Section 3.3 of the wonderfully thorough book Evolutionary Processes in Binary and Multiple Stars by Peter Eggleton. Although the detailed answer to this question is quite involved, the qualitative picture is enlightening, so I will summarize it here. To keep things simple, in this post I am only going to be concerned with conservative mass transfer. This means that no mass or angular momentum is lost in the system — any mass lost from star 1 is accreted by star 2.

The Roche lobe radius and the mass ratio

Let’s consider a binary system in which one star (the “donor”) has filled its Roche lobe and is losing matter to the other star (the “gainer”). As this happens, the donor becomes less massive and the gainer becomes more massive, thereby changing the mass ratio of the system. With the changing mass ratio comes a changing gravitational potential, which in turn means that the Roche lobe itself changes as well.

Now, the Roche lobe itself has a fairly complicated geometry, but we can get a sense for how big it is by integrating to find its volume and then defining an effective radius, \(R_L\), which is the radius of a sphere with the same volume as the Roche lobe. We can then look at how \(R_L\) changes as the mass ratio, \(q\), changes. Peter Eggleton found a nice approximation in 1983 which is better than ~1% in all cases:

This function is monotonic in \(q\), so as the donor loses mass the ratio of the effective Roche lobe radius to the semi-major axis, \(a\), always decreases. This does not quite tell the whole story, however, because in the process of mass transfer the semi-major axis also changes. If the timescale for mass transfer is slow relative to the orbital period, the semi-major axis as function of \(q\) is given by \(a = a_{\min} (1 + q)^4 / 16q^2\). (This condition should almost always be met for semi-detached systems.) The smallest semi-major axis is therefore achieved for equal mass systems, \(q = 1\). If we combine this with the expression for \(R_L\), we find that the physical size of the Roche lobe is given by

which looks like this:

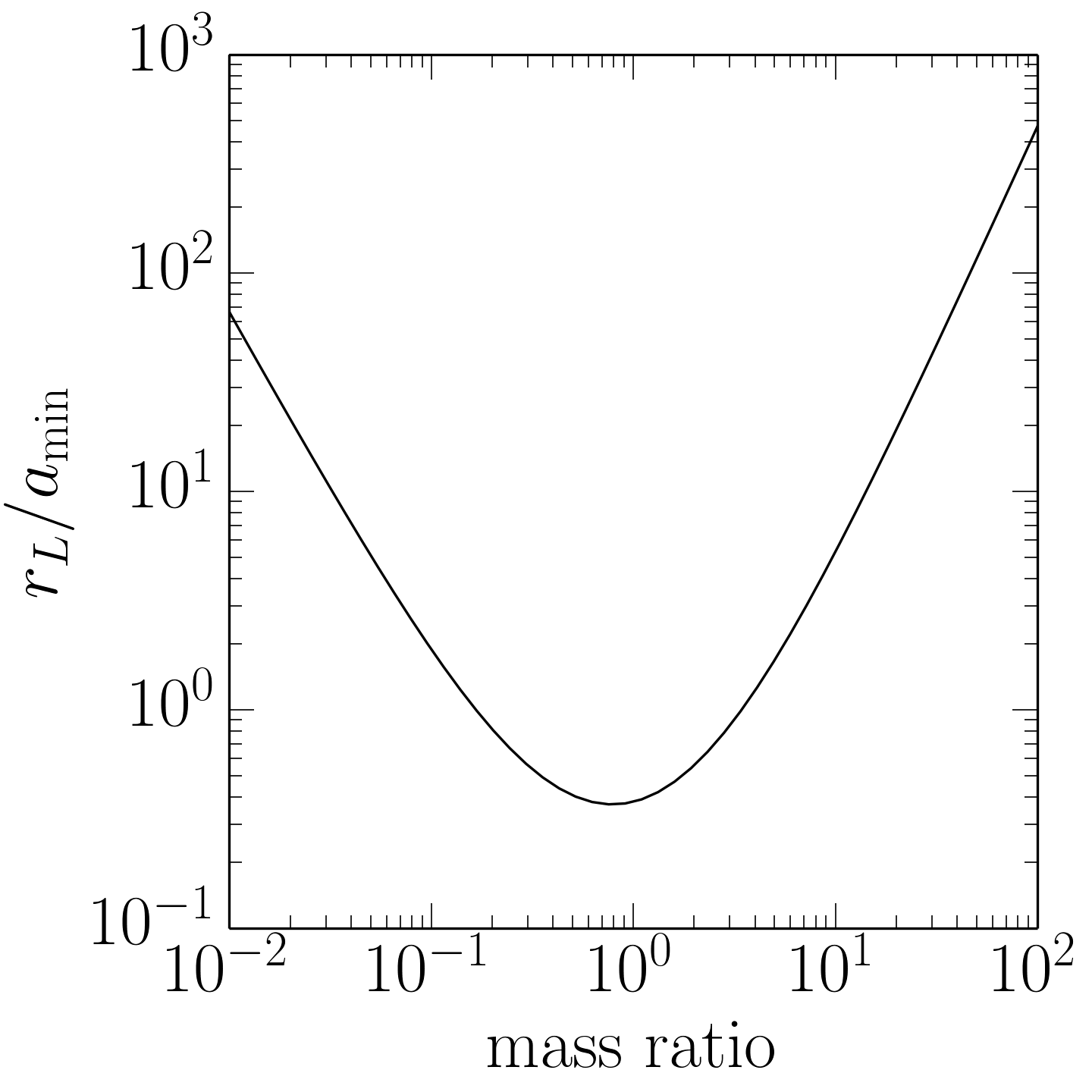
So if the donor is much more massive than the gainer (\(q \gg 1\)), the physical size of the Roche lobe shrinks as the donor loses mass. But if the donor is much less massive than the gainer (\(q \ll 1\)), the increase in the semi-major axis due to the mass loss more than makes up for the decreased ratio \(R_L/a\), so the overall size of the Roche lobe increases.

Timescales

As with any process in astronomy, it is instructive to examine the timescales in the problem. In this case there are three relevant timescales. In order of decreasing time:

1. The nuclear timescale. This is the evolutionary timescale of an isolated star. As the star evolves the composition of the core changes due to nuclear burning. These composition changes lead to changes in the luminosity of the star, and ultimately, its radius. The nuclear timescale is the time for the star to change its core composition by a factor of order unity. For a Sun-like star the nuclear timescale is ~10 Gyr.

2. The thermal timescale. Also known as the Kelvin-Helmholtz timescale, this is the time for the star to lose energy due to gravitational contraction. For a Sun-like star the thermal timescale is ~10 Myr.

3. The hydrodynamic timescale. This is the timescale for a star which has exceeded its Roche lobe to return to the Roche lobe. This timescale can be estimated by using Bernoulli’s equation to calculate the mass flow through the first Lagrange point by modeling the mass transfer as flow through a cylindrical pipe. It is difficult to calculate the hydrodynamic timescale exactly, but it is of order the dynamical time of the star (i.e., the sound crossing time). For a Sun-like star the hydrodynamic timescale is ~1 hour.

The radius-mass relationship

In order to determine which of these three timescales will operate, we must understand how the donor’s radius is related to its radius. The starting point here is the zero-age main sequence (ZAMS) mass-radius relationship, which can be written as

for some constant \(\alpha\). A value like \(\alpha \sim 0.8\) is pretty good for many initial masses, but its specific value isn’t important to us here. The important feature of this relationship is that near any particular mass, the relationship between the mass and radius is approximately a power law.

We next must take into account the fact that the radius of a star slowly changes over time due to changes in its internal composition as hydrogen is consumed and helium produced. This change in radius is approximately exponential — for a Sun-like star, it is a change of \(\sim\)0.7% for every 100 Myr. Since this change in the radius happens over the nuclear timescale, we may incorporate it into our mass-radius relationship as

where \(t_{\textrm{NE}}\) is the nuclear timescale of the star (\(\sim\)10 Gyr for a Sun-like star).

Mass loss on the nuclear timescale

How does this relationship interact with the Roche lobe radius? Suppose the mass-radius relationship is fairly steep, as in the figure below, where we have taken \(\alpha = 3\):

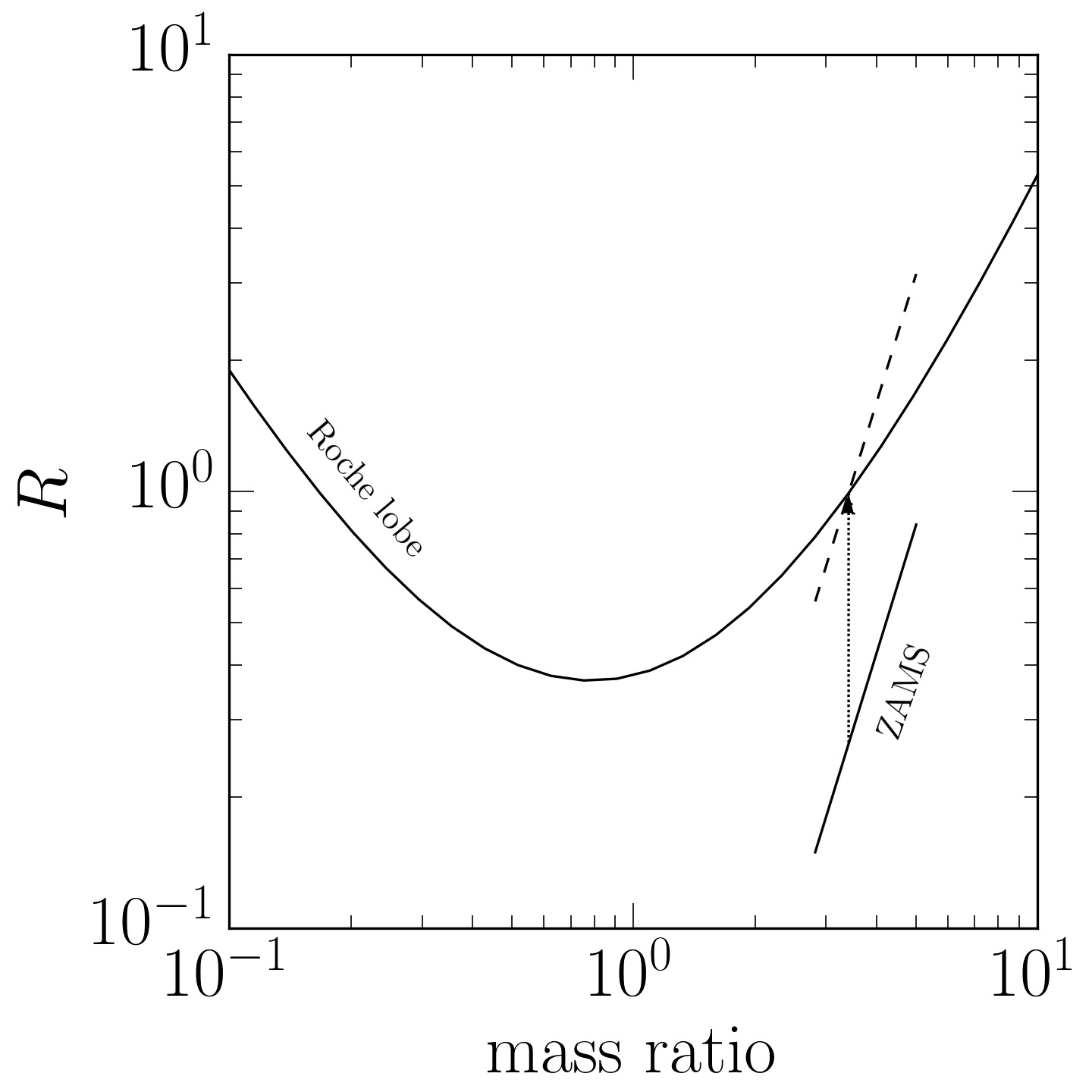
In this scenario, we start out on the ZAMS, and then over the nuclear timescale, the radius of the star slowly increases along the dotted arrow until the radius reaches the Roche lobe. Once the radius increases a little beyond the Roche lobe, that mass is lost to the other star. This pushes the star slightly down the mass-radius relationship, represented by the dashed line. Because the mass-radius relationship is steeper than the Roche lobe relationship at this point, the radius of the star is now well below the Roche lobe after having lost mass. The star must therefore evolve at the nuclear timescale until it expands enough to fill its Roche lobe again. Thus, when the mass-radius relationship is steep relative to the Roche lobe relationship, mass loss proceeds on the nuclear timescale.

Mass loss on faster timescales

Now consider a mass-radius relationship that is much shallower, as in the figure below, where we have taken \(\alpha = .5\):

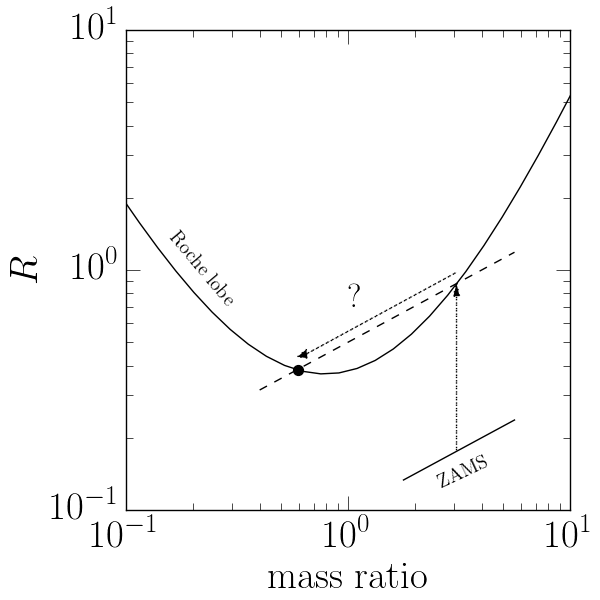
Again we start on the ZAMS, and then move up the dotted arrow on the nuclear timescale as the radius of the star slowly increases due to ordinary stellar evolution. Eventually, the star fills its Roche lobe, at which point it begins losing mass. This causes the star’s mass and radius to decrease, and therefore to move to the left along the dashed line. However, because the mass-radius relationship is above the Roche lobe-mass ratio relationship, the star still finds itself overfilling its Roche lobe even after it has lost some mass. It seems that something catastrophic must happen to the star here. We might imagine that the star would rapidly lose mass, following the dashed line until it once again intersects the Roche lobe-mass ratio relationship. But this is not quite right, because the mass-radius relationship is only valid for stars in thermal equilibrium. Whatever happens to the star in this situation, it is clearly not in thermal equilibrium, and a substantial amount of mass will have to be lost on a timescale that is short compared to the nuclear timescale.

At this point we need to know more about the donor star. In particular, it turns out that the behavior of the mass loss depends on whether the outer envelope of the star is radiative or convective.

Radiative envelopes

Stars with radiative envelopes have shallow temperature gradients relative to the adiabatic temperature gradient. This renders them stable to convection since hot bubbles in the envelope thermalize with their surroundings before they have the chance to move very far under their own buoyancy. In this case, when the star has expanded slightly beyond the Roche lobe, the outer layer will be stripped and the star will no longer be in thermal equilibrium. The star will then require a Kelvin-Helmholtz time to adjust to its new thermal equilibrium beyond the Roche lobe. The mass loss will therefore take place on the thermal timescale.

Convective envelopes

Stars with convective envelopes constantly circulate material throughout the convective envelope on the hydrodynamic timescale. If the outer layer is stripped, the material will be replenished by the star as new convective bubbles rise to its surface. (One can imagine the bubbles as overeager lemmings casting themselves bodily into space as they rise beyond the Roche lobe.) These stars will therefore lose mass on the hydrodynamic timescale

Summary

The three modes of mass transfer are:

1. If the slope of the mass-radius relationship is steep relative to the Roche lobe-mass ratio relationship, mass loss will take place on the nuclear timescale.

2. If the slope of the mass-radius relationship is shallow relative to the Roche lobe-mass ratio relationship and the star’s envelope is radiative, mass loss will take place on the Kelvin-Helmholtz timescale.

3. If the slope of the mass-radius relationship is shallow relative to the Roche lobe-mass ratio relationship and the star’s envelope is convective, mass loss will take place on the hydrodynamic timescale.